Resolvendo o Quadrado Mágico

Se você não é nerd, não gosta de matemática, odeia jogos de lógica ou não gosta de ler textos longos, pule para o próximo post; tem um vídeo muito bom dos barbixas...

----------------------------

Quem já resolveu um quadrado mágico??? Para quem não sabe, quadrado mágico é o seguinte: pegue os números de 1 a 9 e coloque-os em um tabuleiro 3x3 de tal modo que a soma dos três números de cada linha, de cada coluna e de cada diagonal dêem o mesmo resultado.



Não é difícil quanto parece e a maioria das pessoas, depois de tentar algumas combinações e chutes, normalmente chega no resultado.

Hoje, durante uma aula sonolenta, descobri um jeito de chegar no resultado final sem chutar nada!!! Não acrescenta nada à vida de ninguém mas achei bem legal... vamos lá:


Primeiro temos que saber qual será o valor de cada soma. Na 1ª linha, a gente soma 3 números; na 2ª linha, outros 3; e na 3ª linha os outros 3. Ou seja, se a gente somar a soma das 3 linhas no fundo vai ter a soma dos 9 números. Só que a soma de 1 a 9 a gente sabe: 45! (soma de uma p.a. de 9 termos, razão 1 e a0=1). Como todas as linhas possuem a mesma soma, a soma de cada linha será 45/3 = 15!

Sabendo que nós temos que somar 3 números para chegar à 15 em cada linha, coluna e diagonal, vamos ver todas as possibilidades de contas que nós temos (lembrando que não se pode repetir números):

9+5+1=15
9+4+2=15
8+6+1=15
8+5+2=15
8+4+3=15
7+6+2=15
7+5+3=15
6+5+4=15

8 possibilidades. Só que se a gente prestar atenção nós temos 3 linhas, 3 colunas e 2 diagonais, totalizando 8 contas!! Ou seja, exatamente uma conta para cada posição (não pode haver uma conta em duas posições pois isso implicaria em repitir os 3 números dessa conta em dois lugares). Isso significa que, se houver uma solução, vai ser única!

Contabilizando quantas vezes cada número aparece nas contas acima temos que:
Aparecem em 2 contas: 1, 3, 7 e 9
Aparecem em 3 contas: 2, 4, 6 e 8
Aparecem em 4 contas: 5

Olhando para o tabuleiro (ou matriz) 3x3 percebemos que existem 3 posições possíveis:
- Esquina: participam de 3 contas (uma linha, uma coluna e uma diagonal). Existem 4 delas no tabuleiro.
- Lateral: participam de 2 contas (uma linha e uma coluna). Existem 4 deles no tabuleiro.
- Centro: participa de 4 contas (uma linha, uma coluna e duas diagonais). Existe apenas 1 no tabuleiro.

Ou seja, os números que aparecem em 2 contas vão para as laterais, os que aparecem em 3 contas vão para as esquinas e o que aparece em 4 contas vai para o centro. Começamos pelo meio:


Ao acrescentar um número (2, 4, 6 ou 8) numa esquina qualquer, imediatamente já sabemos o número da esquina oposta (pois a soma da diagonal é 15). Nas outras duas esquinas vão os outros dois números de esquina que sobraram. Não importa em qual esquina ele foi colocado; pois o espelhamento do tabuleiro em qualquer direção não altera a soma de colunas linhas ou diagonais. No fundo, como já foi mostrado, só existe uma solução.



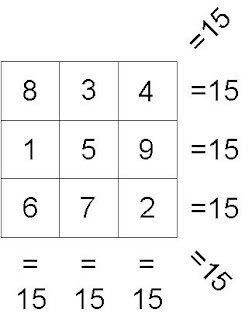
Agora basta preencher as laterais com os números restantes obedecendo aos resultados da soma, que devem ser iguais a 15. Assim completamos o quadrado sem chutar nada:


Não perca nos próximos capítulos: 4x4 (se é que é possível)....